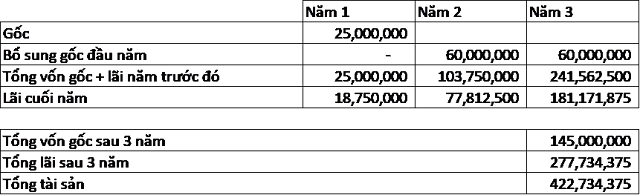Albert Einstein từng phát biểu: “Lãi suất kép là kỳ quan thứ 8 của Thế Giới! những ai hiểu được nó từ đó sẽ kiếm được tiền, ai không hiểu sẽ phải trả chi phí cho điều đó”. Tỷ phú Warren Buffett là một fan trung thành của lãi kép, và ông đã nhận ra vai trò của lãi kép từ rất sớm. Thực ra từ hàng ngàn năm trước lãi suất kép đã được hình thành và con người đã áp dụng một cách triệt để tạo ra lợi nhuận và sự thành công.
Trong tài chính, có thể hiểu đơn giản là sau khi tính lãi từ chu kỳ đầu tiên, khách hàng không nhận lãi mà sẽ gộp chung với tiền gốc để tái đầu tư/đầu tư để tiếp tục nhận lãi cao hơn ở chu kỳ tiếp theo. Do vậy lãi kép phụ thuộc vào yếu tố thời gian và lãi suất.
Người ta thường nói “Lãi mẹ đẻ lãi con” cũng là câu nói đúng về lãi suất kép và cũng chính là mấu chốt của lãi kép khi tận dụng được thời cơ (thời điểm tốt, lãi suất cao).
Từ những lý giải trên, lãi suất kép – Compounding Interest (hay còn gọi là lãi kép) là tái đầu tư lãi. Tức là sau khi sinh lời, lãi đó được dồn vào tiền vốn và đầu tư cho các chu kỳ đầu tư tiếp theo. Vốn và lãi gộp càng nhiều thì lãi suất kép càng có hiệu quả.
Chúng ta hãy cùng nhau xem qua câu chuyện cổ về hạt lúa và bàn cờ vua để dễ hình dung hơn
Chuyện kể rằng, vào thế kỉ thứ 6, ở vương quốc Gupta, (thuộc Ấn Độ) đức vua Sêram trị vì đất nước. Khi đất nước thái bình, muốn tìm kiếm một thú vui tao nhã nào đó để tận hưởng cuộc sống nên đức vua ban bố khắp thiên hạ ai có sáng kiến gì hay thì dâng lên nhà vua. Một hôm, có một nhà thông thái tên là Seta đã dâng lên nhà vua một trò chơi có tên là Saturanga.
Lúc đầu, nhà vua nhìn thấy bàn cờ 64 ô với những quân cờ và nước đi đơn giản nên tỏ ra không hứng thú lắm. Nhưng khi nhà thông thái hướng dẫn cách chơi và cùng chơi với nhà vua đã khiến cho nhà vua vô cùng khâm phục sự sắc sảo và đa dạng của các tình huống trên bàn cờ. Nhà vua đã say mê chơi trò ấy suốt cả tuần trời mà không thấy chán. Quá khâm phục trí tuệ của người sáng tạo, nhà vua quyết định ban thưởng hậu hĩnh. Ngài nói với Seta:
– Ta muốn tặng thưởng cho ông một cách xứng đáng. Nào, Seta, ông hãy nói điều ông muốn ta ban thưởng cho ông. Đừng ngại, hãy nói ra phần thưởng có thể làm ông thỏa mãn và ông sẽ nhận được nó ngay lập tức. Ta rất giàu có và không tiếc gì để có thể ban thưởng cho ông một cách xứng đáng.
Seta im lặng suy nghĩ. Nhìn nhà vua chờ đợi câu trả lời, ông biết nhà vua không nói đùa. Lúc sau ông chậm rãi thưa:
– Thưa đức vua, lòng tốt của ngài thật vĩ đại. Nhưng vì đột ngột quá nên thần chưa nghĩ ra được điều gì. Xin ngài cho thần nghĩ đến sáng ngày mai.
Nhà vua mỉm cười gật đầu đồng ý.
Sáng sớm hôm sau, như đã hứa, Seta vào gặp nhà vua. Sự khiêm tốn của Seta khiến nhà vua hết sức cảm mến. Seta cung kính thưa:
– Thưa đức vua! Thần không ham gì vàng bạc châu báu. Chỉ xin ngài thực hiện cho thần một điều ước.
– Người cứ nói. Ta chắc chắn rằng, mọi điều ước của người sẽ được đáp ứng.
– Thưa ngài! Ngài hãy ra lệnh cho đặt 1 hạt lúa mì vào ô thứ nhất của bàn cờ. Seta nói.
– Chỉ đơn giản thế thôi ư ? Nhà vua kinh ngạc.
– Vâng, thưa ngài. Tiếp đến, ở ô thứ 2, ngài hãy đặt vào 2 hạt thóc.
– Ô! Nhà vua không kìm chế nổi sự kinh ngạc của mình:
– Này Seta, ông đang đùa ta đấy ư? Làm như thế có ý nghĩa gì?
Seta chậm rãi trình bày tiếp:
– Kính thưa đức vua vĩ đại! Cứ như cách làm vừa rồi, ô tiếp sau sẽ có số thóc gấp đôi ô trước cho đến ô cuối cùng. Thần sẽ nhận lấy toàn bộ số thóc đó.
– Thật không có gì khó. Kho thóc của ta có thể nuôi toàn bộ dân chúng trong nhiều năm mà không phải làm gì. Seta, ông thật khiêm tốn.
Seta cung kính vái lạy cảm ơn và xin phép ra về, hẹn đến ngày nhà vua đếm xong số thóc sẽ đến nhận lấy.
Một tuần sau, nhà vua lại gọi Seta vào cùng chơi cờ. Lúc đang chơi, nhà vua hỏi:
– Seta, hẳn ông đã hài lòng về phần thưởng của ta. Ông đã mang đủ số thóc về rồi chứ?
Seta thưa:
– Dạ, bẩm đức vua, các nhà toán học cung đình vẫn đang tính tiếp số thóc cho thần ạ.
– Ngươi hãy yên tâm – Nhà vua nói. Có lẽ các quan đã làm việc chậm trễ. Ta sẽ thúc đẩy việc này và người sẽ sớm nhận được phần thưởng như ta đã hứa.
Sau đó, các quan vào tâu với đức vua về con số khủng khiếp mà Seta đã yêu cầu. Toàn bộ số thóc trên vương quốc đã được huy động mà vẫn chưa đủ đến một phần số thóc ấy. Nhà vua vô cùng sửng sốt, chú ý những lời nói của nhà toán học già nua.
– Hãy nói cho ta con số quái gở đó. Nhà vua trầm ngâm.
– Nếu đếm đủ số thóc đến ô thứ 64 của bàn cờ thì là 18 tỉ tỉ 446 triệu tỉ 774 ngàn tỉ 73 tỉ 709 triệu 551 ngàn 615 hạt. (18.446.744.073.709.551.615). Nếu huy động cả các nước lân cận thì vẫn không đủ. Nếu phải tăng diện tích sản xuất, tích trữ nhiều năm cũng vẫn không thể có đủ số thóc ấy được .Mong nhà vua suy xét.
– Trời. Seta. Ngươi thật trí tuệ!
Nhà vua quay lại hỏi quan coi kho:
– Vậy phải làm thế nào đây ? Nếu ta quyết định thưởng theo yêu cầu thì Vương quốc vĩnh viễn mắc nợ người ta, không biết bao giờ mới trả được hết nợ. Còn nếu không thưởng như vậy, thì Trẫm là kẻ không biết giữ lời hứa, còn mặt mũi nào trước bàn dân thiên hạ nữa !.
Suy nghĩ một lúc, vị quan tâu:
– Seta đã tính được con số ấy. Có một cách đơn giản, xin nhà vua yêu cầu Seta tự mình đếm số thóc của từng ô và mang số thóc ấy về, không được thiếu hay thừa một hạt nào.
– Nếu Seta đồng ý làm việc áy thì sẽ mất bao lâu. Nhà vua sốt sắng hỏi.
– Dạ bẩm đức vua! Seta phải cần đến 290 tỉ năm.
Đến lúc này, Nhà vua không khỏi kinh ngạc tột độ trước sức mạnh trí tuệ của Seta.
Sau đó, nhà vua gọi Seta vào và yêu cầu làm việc ấy. Seta khiêm tốn trình bày:
– Thần chỉ muốn cho nhà vua biết bài toán ấy chứ thực không dám nhận số thóc như yêu cầu. Xin nhà vua trị tội vì thàn đã bất kính.
Khâm phục trí tuệ và đức khiêm tốn của Seta ta, sau đó, nhà vua phong ông làm tể tướng, cùng nhà vua trị vì đất nước.
Số hạt lúa trên bàn cờ vua và bài toán lãi suất kép
Quay lại bài toàn phía trên, nếu tính theo cấp lũy thừa thì bài toán hát lúa trên bàn cờ vua này sẽ được tính như sau:
Ta có:
Ô thứ 1: Có số lúa 2^0 = 1
Ô thứ 2: Có số lúa 2^1 = 2
Ô thứ 3: Có số lúa 2^2 = 4
Ô thứ 4: Có số lúa 2^3 = 8
…
Ô thứ 64: Có số lúa là 2^63
Gọi S là tổng số lúa, thì ta có số hạt lúa là:
S = 2*(2^0 + 2^1 + 2^2+ 2^3 + ….+ 2^62+ 2^63)
2S = 2*(2^0 + 2^1 + 2^2+ 2^3 + ….+ 2^62+ 2^63)
2S = 2^1 + 2^2+ 2^3 + 2^4 ….+ 2^63+ 2^64
S= 2S-S =2^64 – 2^0
Như vậy, số hạt lúa chính xác mà nhà vua cần trả là:
S = 2^61-1 = S=2^64−1 = 18,446,744,073,709,551,615 (hạt lúa) – 18,4 tỷ tỷ hạt lúa!
Như vậy, tính lên nó sẽ là con số bao nhiêu tấn gạo? Một hạt gạo nặng trung bình là 0.029 grams, như vậy nếu quy ra số lúa trên tương đương: 536 tỷ tấn gạo!
Tổ chức Nông Lương Liên Hiệp Quốc (FAO) ước tính tổng sản lượng ngũ cốc (gạo là 1 trong 5 loại ngũ cốc) thế giới năm 2020 khảng 7.18 tỷ tấn. Như vậy số lúa gạo mà người dân kia đòi nhà vua thường bằng số lương thực toàn bộ loài người hiện đại chúng ta sản xuất trong gần 75 năm!
Lãi kép trong đầu tư tài chính
Khái niệm về lãi suất kép khá đơn giản, và trên thực tế khi áp dụng nhiều khách hàng cho rằng không nhận thấy sự khác biệt nào so với các cách tính lãi suất thông thường.
Tuy nhiên, vì lãi suất kép dựa trên cả nguyên lý thời gian và lãi suất nên chỉ khi đầu tư trong thời gian đủ dài, số tiền lãi tự đẻ ra sẽ là con số lớn khổng lồ, khiến bạn hoàn toàn bất ngờ.
Ví dụ một bài toán của tài chính truyền thống
Giả sử anh Nguyễn Văn A 25 tuổi, mỗi tháng anh tiết kiệm được 1 triệu/tháng và gửi nó vào ngân hàng. Anh liên tục gửi tiền tiết kiệm trong vòng 20 năm, vậy đến khi anh 45 tuổi anh nhận được bao nhiêu tiền (tính cả gốc lẫn lãi)?
Đáp án: Anh sẽ nhận được tổng cộng là 498,412,096 VNĐ (gồm 240,000,000 tiền gốc và 258,412,096 tiền lãi) khi đầu tư suốt 20 năm trên.
Hoặc một bài toán của thị trường crypto
Chị Trần Thị T cũng 25 tuổi, quyết định đầu tư vào thị trường crypto cùng Hên Network với lợi nhuận cam kết 75%/năm. Chị bắt đầu với số vốn nhàn rỗi là 25 triệu. Hàng tháng chị vẫn tiết kiệm được khoảng 5 triệu, tương đương có thêm 60 triệu/năm tiền nhàn rỗi.
Hết năm thứ 1, phần lời của chị là 18 triệu 750 nghìn, chị quyết định, bổ sung thêm vốn gốc từ tiền tiết kiệm của mình. Lúc này phần gốc của chị T đã là 60 triệu, lợi nhuận 18 triệu đô, tổng cộng 103 triệu 750 nghìn.
Hết năm thứ 2, phần lời của chị T là khoảng 77 triệu. Trong đó hơn 14 triệu là thuần lời từ lãi của năm 1. Chị tiếp tục bổ sung thêm vốn gốc từ tiền tiết kiệm của mình. Lúc này tổng cả vốn lẫn lãi của chị là hơn 241 triệu.
Hết năm thứ 3, tiền lời của chị T đã vào khoảng 181 triệu, tổng cả vốn lẫn lời là hơn 422 triệu.
Kết luận, so với anh A, chị T có thể khó khăn hơn trong giai đoạn đầu do phải tiết kiệm nhiều hơn, nhưng nhờ tận dụng đúng kênh đầu tư, cùng với sức mạnh của lãi kép, chị T đã đạt được kết quả tương đương anh A chỉ trong vòng hơn 3 năm.
Làm thế nào để tận dụng lãi kép
Hãy bắt đầu tiết kiệm từ sớm
Tài không đợi tuổi, đầu tư cũng vậy. Dù bạn bao nhiêu tuổi, bạn cũng nên đưa ra quyết định đầu tư ngay. Chỉ cần một số tiền đầu tư nhỏ ban đầu, qua thời gian lãi suất kép sẽ biến nó trở thành món tiền lớn theo cấp số nhân.
Hãy tiết kiệm thường xuyên
Đừng ngắt quãng mà thay vào đó là cố gắng đầu tư liên tục. Lên kế hoạch chi tiêu rõ ràng và để dành tiền nhàn rỗi của mình và đầu tư trong ngân hàng. Hãy ghi nhớ rằng lãi kép chỉ có tác dụng khi số tiền gửi của bạn có cơ hội sinh sôi.
Không được trì hoãn
Trì hoãn là sai lầm nghiêm trọng mà nhiều khách hàng mắc phải khi đầu tư tiết kiệm. Cái giá của việc trì hoãn được thể hiện qua con số nhận được, trì hoãn càng nhiều số tiền nhận được sẽ càng ít đi.
—–
Đó là lý do tại sao thiên tài Albert Einstein nói: “Lãi suất kép là kỳ quan thứ 8 của Thế Giới. Những ai hiểu được nó từ đó sẽ kiếm được tiền, ai không hiểu sẽ phải trả chi phí cho điều đó”.